熟悉熟悉公式插件，整理整理学习LDA模型的时候对参数推导的理解，与原始论文有所不同。
模型定义
具体定义参考原始论文,这里使用平滑模型，对topic-word也加了先验信息。
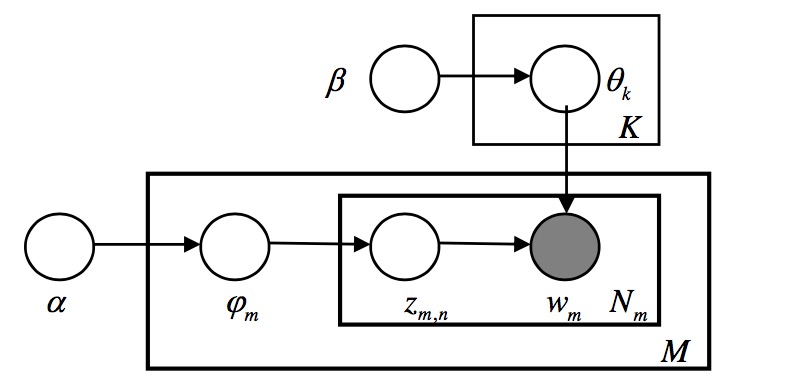LDA图模型
引理
在推导时候需要用几个引理
引理1.
定义相对熵 \begin{equation} KL(q(z),p(z|w)) = \sum_zq(z)ln\frac{q(z)}{p(z|w)} \end{equation}
那么有公式 \begin{equation} lnp(w) = \mathcal{L}(q)+KL(q(z),p(z|w)) \end{equation}
其中
\begin{equation} \mathcal{L}(q)=\sum_zq(z)ln\frac{p(z,x)}{q(z)} \end{equation} 证明：
\begin{split}
&\sum_zq(z)ln\frac{p(z,w)}{q(z)}+\sum_zq(z)ln\frac{q(z)}{p(z|w)} \\
&=\sum_zq(z)ln\frac{p(z,w)}{p(z|w)} \\
&=\sum_zq(z)lnp(w) \\
&=lnp(w)
\end{split}
证毕■
引理2
$ \arg\underset{q}{\rm min}KL(q(z),p(z|w)) $ 等于 $ \arg\underset{q}{\rm max}\mathcal{L}(q) $.
证明：
\begin{split}
\arg\underset{q}{\rm min}KL(q(z),p(z|w)) &=>
\arg\underset{q}{\rm min}(-\sum_zq(z)ln\frac{p(z|w)}{q(z)}) \\
&=>\arg\underset{q}{\rm max}(\sum_zq(z)ln\frac{p(z|w)}{q(z)}) \\
&=>\arg\underset{q}{\rm max}(\sum_zq(z)ln\frac{p(z,w)}{q(z)}) \\
&=>\arg\underset{q}{\rm max}\mathcal{L}(q)
\end{split}
证毕■
$p(z|w)$ 和 $p(z,w)$都是常量，且都大于0。
变分贝叶斯求解
原始论文使用极大似然求参。
现在推导LDA的变分推断。
对数似然函数
\begin{equation}
\begin{split}
lnL(\alpha,\beta)&=\sum_{m=1}^{M}L(W_m;\alpha,\beta) \\
&=\sum_{m=1}^{M}(\mathcal{L}(\lambda,\phi_m,\gamma_m) + KL(q(\varphi_m,z_m,\theta;\lambda,\phi_m,\gamma_m),
p(\varphi_m,z_m,\theta|W_m;\alpha,\beta))
\end{split}
\end{equation}
其中
\begin{equation}
\begin{split}
\mathcal{L}(\lambda,\phi_m,\gamma_m)&=\int\sum_zq(\varphi_m,z_m,\theta;\lambda,\phi_m,\gamma_m)
ln\frac{p(\varphi_m,z_m,\theta,W_m;\alpha,\beta)}{q(\varphi_m,z_m,\theta;\lambda,\phi_m,\gamma_m)}\,d\varphi_m\,d\theta_m \\
&=E_q[lnp(\varphi_m,z_m,\theta,W_m;\alpha,\beta)]-E_q[lnq(\varphi_m,z_m,\theta;\lambda,\phi_m,\gamma_m)]
\end{split}
\end{equation}
需要最大化$lnL(\alpha,\beta)$和最小化$KL(q(\varphi_m,z_m,\theta;\lambda,\phi_m,\gamma_m), p(\varphi_m,z_m,\theta|W_m;\alpha,\beta))$，根据引理2，这等同于最大化最大化$\mathcal{L}(\lambda,\phi_m,\gamma_m)$.
即现在目标为$\arg\underset{q}{\rm max}\mathcal{L}(\lambda,\phi_m,\gamma_m)$.
求解，平均场理论来近似概率分布，定义
\begin{equation} q(\varphi,z,\theta)=\prod_{k=1}^{K}q(\theta_k;\lambda_k)\prod_{m=1}^{M}q(\varphi_m;\gamma_m) \prod_{m=1}^{M}\prod_{n=1}^{N_m}q(z_{m,n};\phi_{m,n}) \end{equation}
其中$\lambda$和$\gamma$是Dirichlet分布参数，$\phi$是多项分布参数，
得到
\begin{equation}
\begin{split}
\mathcal{L}(\lambda,\phi_m,\gamma_m)=&E_q[lnp(\theta)]+E_q[lnp(\varphi_m)]+ \\
&E_q[lnp(z_m|\varphi_m)]+E_q[lnp(W_m|\varphi_m,z_m,\theta)]- \\
&E_q[lnq(\varphi_m)]-E_q[lnq(z_m)]-E_q[lnq(\theta)]
\end{split}
\label{eql}
\end{equation}
现在将\eqref{eql}展开，每一项展开
\begin{equation}
\begin{split}
E_q[lnp(\theta)]&=\int q(\theta)lnp(\theta)d(\theta) \\
&=\int\prod_{k=1}^{K}q(\theta_k;\lambda_k)ln\prod_{k=1}^{K}p(\theta_k;\beta)d\theta \\
&=\sum_{k=1}^{K}\int q(\theta_k;\lambda_k)lnp(\theta_k;\beta)d\theta_k \\
&=\sum_{k=1}^{K}\int Dir(\theta_k;\lambda_k)ln\frac{1}{B(\beta)}\prod_{v=1}{V}\theta_{k,v}^{\beta_v-1}d\theta_k \\
&=\sum_{k=1}^{K}\int Dir(\theta_k;\lambda_k)ln\frac{1}{B(\beta)}d\theta_k
+\sum_{v=1}^{V}(\beta_v-1)\int Dir(\theta_k;\lambda_k)ln\theta_{k,v}d\theta_k \\
&=\sum_{k=1}^{K}ln\frac{1}{B(\beta)}+\sum_{v=1}^{V}(\beta_v-1)E_q[ln\theta_{k,v}] \\
&=\sum_{k=1}^{K}ln\Gamma(\sum_{v=1}^{V}\beta_v)-\sum_{v=1}^{V}ln\Gamma(\beta_v)
+\sum_{v=1}^{V}(\beta_v-1)(\Psi(\lambda_{k,v})-\Psi(\sum_{k=1}^{K}\lambda_{m,k}))
\end{split}
\end{equation}
同理
\begin{equation} \begin{split} E_q[lnp(\varphi_m)]=ln\Gamma(\sum_{k=1}^{K}\alpha_k)-\sum_{k=1}^{K}ln\Gamma(\alpha_k) +\sum_{k=1}^{K}(\alpha_k-1)(\Psi(\gamma_{m,k})-\Psi(\sum_{k=1}^{K}\gamma_{m,k})) \end{split} \end{equation}
\begin{equation}
\begin{split}
E_q[lnp(z_m|\varphi_m)]&=\int\int q(z_m,\varphi_m)lnp(z_m|\varphi_m)dz_md\varphi_m \\
&=\int\int q(z_m;\phi_m)Dir(\varphi_m;\gamma_m)lnMult(z_m;\varphi_m)dz_md\varphi_m \\
&=\int\int q(z_m;\phi_m)Dir(\varphi_m;\gamma_m)ln\varphi_{m,z_m}dz_md\varphi_m \\
&=\int\prod_{n=1}^{N_m}Mult(z_{m,n};\phi_{m,n})\int Dir(\varphi_{m,z_m};\gamma_m)ln\varphi_{m,z_m}dz_{m,n} \\
&=\sum_{n=1}^{N_m}\sum_{k=1}^{K}\phi_{m,n,k}(\Psi(\gamma_{m,k})-\Psi(\sum_{k^`=1}^{K}\gamma_{m,k^`}))
\end{split}
\end{equation}
…
…
其余推导公式省略（太难输入了）
最后得到展开的公式，求最大值，令$\mathcal{L}(\lambda,\phi_m,\gamma_m)$的微分为0
省略
省略
误差分析
变分参数估计几处都用了近似（模型、分布、参数…）
\todo 有时间再说
